Design Criteria
General
The Design of drainage system should generally follow the guidelines recommended in CPHEEO manual on Sewerage and Sewage Treatment or other relevant codes with proper justification for deviation or modification. The design of the drainage system requires following:
- Calculating the total discharge that the system require to drain off
- Fixing the slope & dimensions of the drain to have adequate capacity to carry the discharge and afford proper maintenance
Calculation for Discharge
The discharge is dependent upon intensity and duration of precipitation, characteristics of the area and time required for such flow to reach the drain. The storm water flow for the purpose may be determined by using the rational method, hydrograph method, rainfall runoff correlation studies and empirical formulae. The rational method is most commonly used and serves the purpose for design of drain satisfactorily.
The entire storm water would not reach the Storm Water Drainage (SWD). Fraction of it would flow to SWD, which depends on the imperviousness, topography, shape of the drainage basin and duration of the storm. This imperviousness is quantified by a coefficient of runoff, which needs to be determined for each sub-catchment of the drain. The peak runoff at any given point is calculated using the following rational formula.
Qp = Cs CIA/360
| Where, : | Qp - peak flow in m3 /sec |
| C – Runoff coefficient | |
| I – design rainfall intensity mm/hr | |
| A – Contributory area in hectares | |
| Cs – storage coefficient | |
- Coefficient of Runoff
- Time of Concentration
- Imperviousness
- Intensity of Rainfall
Coefficient of Runoff
As runoff is directly proportional to the value assigned to “C”, the proper selection of this value is critical for storm water runoff calculations. Care has to be exercised in selecting this value as it incorporates all of the hydrological extractions, surface imperviousness and antecedent conditions. The values for “C” have been followed as listed in the Table 1 (Manual for Sewerage and Sewage Treatment, CPHEEO).
Runoff Coefficients “C”
Duration, t, minutes |
10 |
20 |
30 |
45 |
60 |
75 |
90 |
100 |
120 |
135 |
150 |
180 |
Weighted Average Coefficients |
||||||||||||
1) Sector concentrating in stated time |
|
|||||||||||
(a) Impervious |
0.525 |
0.588 |
0.642 |
0.7 |
0.74 |
0.771 |
0.795 |
0.813 |
0.828 |
0.84 |
0.85 |
0.865 |
(b) 60% Impervious |
0.365 |
0.427 |
0.477 |
0.531 |
0.569 |
0.598 |
0.622 |
0.641 |
0.656 |
0.67 |
0.682 |
0.701 |
(c) 40% Impervious |
0.285 |
0.346 |
0.395 |
0.446 |
0.482 |
0.512 |
0.535 |
0.554 |
0.571 |
0.585 |
0.597 |
0.618 |
(d) Pervious |
0.125 |
0.185 |
0.23 |
0.277 |
0.312 |
0.33 |
0.362 |
0.382 |
0.399 |
0.414 |
0.429 |
0.454 |
2) Rectangle (length = 4 x width) concentrating in stated time |
||||||||||||
(a) Impervious |
0.55 |
0.648 |
0.711 |
0.768 |
0.808 |
0.837 |
0.856 |
0.869 |
0.879 |
0.887 |
0.892 |
0.903 |
(b) 50% Impervious |
0.35 |
0.442 |
0.499 |
0.551 |
0.59 |
0.618 |
0.639 |
0.657 |
0.671 |
0.683 |
0.694 |
0.713 |
(c) 30% Impervious |
0.269 |
0.36 |
0.414 |
0.464 |
0.502 |
0.53 |
0.552 |
0.572 |
0.588 |
0.601 |
0.614 |
0.636 |
(d) Pervious |
0.149 |
0.236 |
0.287 |
0.334 |
0.371 |
0.398 |
0.422 |
0.445 |
0.463 |
0.479 |
0.495 |
0.522 |
Time of Concentration
Time of concentration is the longest time required for a particle to travel from the watershed divide to the watershed outlet. The remotest point in each zone is found out and then the level difference between the remote point and the point of discharge is calculated. As per Kirpich Time of Concentration (in minutes) Equations:
tc = 0.078(L0.77/S0.385
| Where, : | L= the distance from the critical point to the point at which discharge is to be estimated in meters. |
S = Slope of the catchment area. |
|
Imperviousness
The impervious cover percentage of the drainage area can generally be obtained from the records of a particular district. In the absence of such data, presented below may serve as the guide (As per CPHEEO Manual on Sewerage and Sewage Treatment):
Sl. No. |
Type of area |
% of impervious cover |
1 |
Commercial & Industrial area |
70 to 90 |
2 |
Residential area |
|
|
i) High Density |
60 to 75 |
|
ii) Low Density |
35 to 60 |
3 |
Parks & Underdeveloped areas |
10 to 20 |
Intensity of Rainfall
It has been observed that shorter the duration of critical rainfall, the greater would be the expected average intensity during that period. The critical duration of rainfall will be which produces maximum runoff. The duration is equal to the time of concentration, since shorter period do not allow the whole area to contribute water, and longer duration will give smaller average rainfall intensity. As such a relationship between time of rainfall duration and probable or expected rainfall intensity has to be developed. The rainfall intensity depend on design return period and time of concentration. The details for calculation of the rainfall intensity has been described in section of rainfall analysis
Intensity of Rainfall for Duration
Duration (t) in min |
Intensity (i) in mm/hour (For 1 year freq) |
2 |
2286 |
3 |
1242 |
4 |
805 |
5 |
575 |
10 |
203 |
15 |
110 |
20 |
71 |
25 |
51 |
30 |
39 |
35 |
31 |
40 |
25 |
45 |
21 |
50 |
18 |
55 |
16 |
60 |
14 |
70 |
11 |
80 |
9 |
90 |
7 |
100 |
6 |
110 |
5 |
120 |
5 |
150 |
3 |
180 |
3 |
Rainfall Analysis
The basic design parameters have to be predetermined so as to analyse the carrying capacity of existing drains and also for the design of new drains. The parameters for determining the rainfall intensity are as follows
- i.Frequency of storm / return period
Sl No. |
Type of area |
Storm frequency |
1 |
Residential areas |
|
|
i) Peripheral area |
Twice a year |
|
ii) Central and comparatively high priced area |
Once a year |
2 |
Commercial and high priced area |
Once in two years |
- ii.Depth –duration of storm
- iii.Time of concentration
- iv.Run off coefficient for the project area
Input Requirement |
Data Source |
Hourly rainfall data of the city or nearby town |
Indian Meteorological Department, Local municipal office, State Water resource department |
- Frequency of storm / return period
- Rainfall Intensity and Duration
- Frequency of Storm.
- Rainfall Intensity from Occurrences
- Calculation for intensity of rainfall
Frequency of storm / return period
The cost of any drainage structure depends on its size, which depends heavily on the return period to be adopted. This depends on the level of protection that is deemed to be adequate for reducing the potential cost of flood damages and minimising inconvenience to the public. Where the potential for damages is low or costs are small a short design return period is usually considered adequate. Return period or frequency of storm for which the storm drains are designed depends on the importance of the area to be drained. Storm Frequency criterion has been adopted as per Table 3 (Ref: CPHEEO Manual for Sewerage and sewage Treatment). For normal cities, 1 year return period may be adopted.Sorted Rainfall Occurrences
Duration |
Precipitation in mm |
||||||||||||
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
50 |
60 |
75 |
100 |
125 |
|
15 min |
346 |
346 |
344 |
319 |
265 |
229 |
177 |
162 |
79 |
72 |
66 |
63 |
46 |
30 min |
256 |
252 |
206 |
151 |
73 |
44 |
44 |
37 |
18 |
17 |
10 |
10 |
7 |
45 min |
128 |
95 |
37 |
24 |
24 |
18 |
12 |
8 |
4 |
2 |
2 |
2 |
0 |
60 min |
58 |
31 |
16 |
15 |
13 |
13 |
12 |
8 |
7 |
7 |
3 |
3 |
2 |
75 min |
38 |
13 |
13 |
12 |
11 |
9 |
6 |
5 |
0 |
0 |
0 |
0 |
0 |
90 min |
12 |
4 |
3 |
3 |
2 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Rainfall Intensity and Duration
The rainfall intensity in mm/hr depends on design return period and on the time of concentration of the storm water flow to reach the section being designed. For this, rainfall intensity duration curve for each city has to be developed based on historical rainfall data, and use them for determining the appropriate rainfall intensity for use in the rational formula. From the rainfall data record, rainfall intensities corresponding to storms of 1,2,5
Frequency of Storm.
The amount of precipitation obtained from the rainfall data for 15, 30, 45, 60, 75 and 90 minutes are sorted in number of occurrences with 10mm, 15mm, 20mm, 25mm, 30mm, 35 mm, 40mm, 45mm, 50mm, 55mm, 60mm, 75mm, 100mm, 125mm. Table 4 presents the total counts of such occurrences over a period of 24 years (as available, here 24 year data was available) obtained by summation of the corresponding values.Rainfall Intensity from Occurrences
From the sorted rainfall occurrences, the cascades for 1 year (24 occurrences), 2 year (12 occurrences) and storm frequency for different return period may be developed by interpolating the higher and lower numbers of occurrences with corresponding maximum and minimum amount of precipitation, the precipitation along the cascade line is obtained. Table 5 presents the cascade for 1 year storm frequency. Sample calculation of intensity corresponding to rainfall duration of 30 minutes: 40 + (45-40)*(22-18) / (37-18) = 41.05 mm/hrCascade for 1 year
Duration (t) (min.) |
Higher No. of Occurrences |
Lower No. of Occurrences |
Intensity (mm/hr) Corresponding to Higher No. of Occurrence |
Intensity (mm/hr) Corresponding to Lower No. of Occurrence |
Intensity (i) (mm/hr) |
15 |
46 |
17 |
75 |
100 |
79.31 |
30 |
37 |
18 |
40 |
45 |
41.05 |
45 |
37 |
24 |
15 |
20 |
14.23 |
60 |
31 |
16 |
10 |
15 |
12.00 |
75 |
38 |
13 |
5 |
10 |
6.80 |
RMSD for 1 Year
Duration (t) (min) |
X =log t |
Y =log i |
X^2 |
XY |
|
I = a/t^m |
15 |
1.176 |
1.981 |
1.383 |
2.33 |
m =1.50564 |
110.054 |
30 |
1.477 |
1.643 |
2.182 |
2.427 |
Log a = 3.812 |
38.758 |
45 |
1.653 |
1.426 |
2.733 |
2.357 |
a =6492 |
21.049 |
60 |
1.778 |
1.114 |
3.162 |
1.981 |
|
13.65 |
75 |
1.875 |
0.914 |
3.516 |
1.713 |
|
9.755 |
|
∑ X = 7.95964 |
∑ Y =7.07752 |
∑ X2 =12.9759 |
∑ XY =10.8081 |
|
|
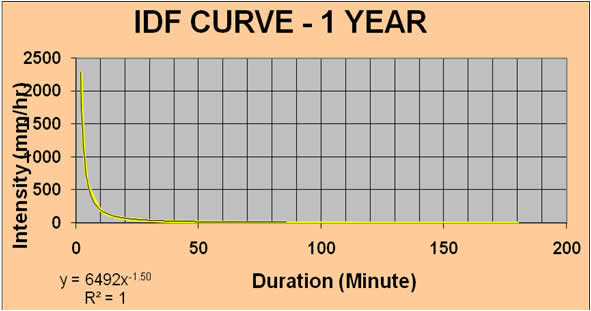
Calculation for intensity of rainfall
Once the intensity of rainfall is obtained, Root Mean Square Deviation (RMSD) calculation for the respective storm return period is carried out to obtain the values of the constants of the empirical expression given by Metcalf and Eddyi = a/ tm
Where : |
i = Intensity of rainfall (mm/hr) |
a,m = Constant |
|
t = Duration (min.) |
|
Table 6 shows the calculation for above equation Based on above, Intensity Duration Frequency curve has been plotted. Based on the curve, Table 7 shows the intensity for various duration. |
|
Adequacy of Drains and Drainage System
According to the basin characteristics, coefficient of runoff, intensity of rainfall corresponding to the time of concentration, the discharge at each section has to be calculated.
- Hydraulic Analysis
- Adequacy
Hydraulic Analysis
The purpose of the hydraulic analysis was to evaluate the adequacy of the existing storm drainage system (major drains only) and to determine design options for inadequately sized channels. Channels and storm drains were simulated using the flow data generated in the hydrology model. Storm drains were simulated using Manning’s equation as below:
V = 1/n x R2/3 x S1/2
Where, |
iV = Velocity (m/s); |
n = Friction Factor; |
|
| R = Hydraulic Radius (m); | |
| and S = Channel Slope (m/m) | |
Adequacy
These storm water design discharge are compared with the carrying capacity of the existing drains. In case the existing sections were found inadequate, the appropriate solution of increasing the capacity has to be done.
Design Considerations
It is desirable to start the design considering the levels at the outfall of drainage locations of drainage system so that the level and bed slopes of the drain are fixed accordingly as per outfall. To allow discharge to pass using gravity flow. In some location pumping may be required. These need to be critically examined.
It may not be possible to take up the work for the whole city at a time and the work may have to be prioritised. The method of priortizing can be:
- Flood prone areas
- City centre, commercial centre and densely populated areas
- Areas where quality of ground water is adversely affected by permeable storm water

